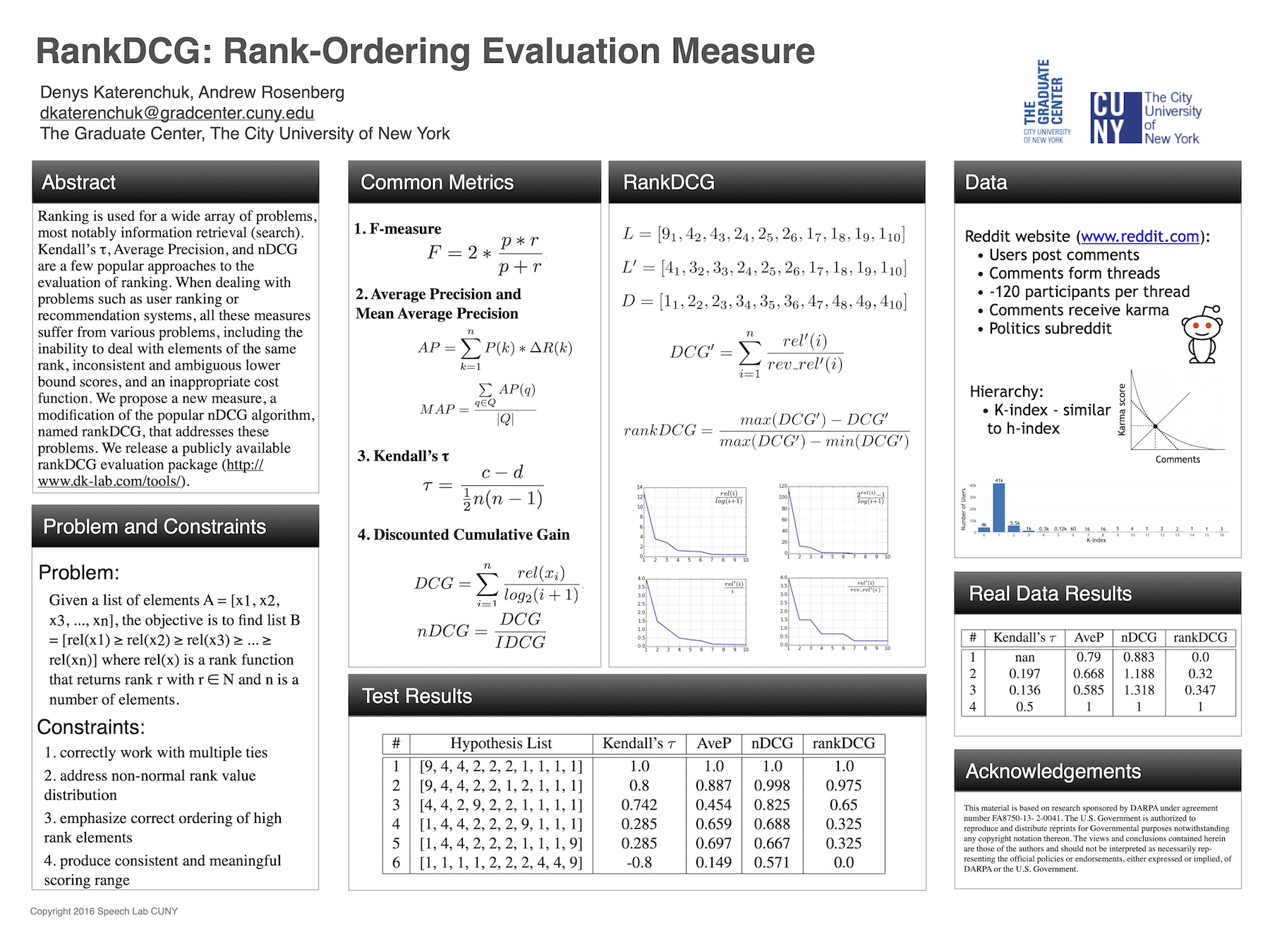
Advanced algorithms improve our lives in subtle, but consistent ways. Google search results seldom make us go to the second page and Netflix magically recommends an interesting movie. These are outcomes of multiple trials and errors to find the best recommendation algorithm. How do these companies determine which algorithm is the best? Evaluating different ranking algorithms is not a trivial task. This is why we developed the Rank Discounter Cumulative Gain (RankDCG) evaluation measure.
The Problem with Current Measures
This measure is designed to evaluate and compare rank-ordering algorithms. RankDCG has three fundamental properties:
- Consistent bounds: Lower and upper score bounds between 0 and 1
- Distribution flexibility: Works with non-normal element distributions
- Transitivity: Allows element transitivity inside sub-groups of the same rank
RankDCG works on a large variety of problems where conventional measures fail.
Information Retrieval Context
Problems such as search or recommendation are defined by the umbrella term information retrieval (IR). These problems deal with retrieving and ranking/ordering relative data, whether it is movies or web pages. This data often comes from a large data source. In order to know which of the items is more relevant, there exists a function, we can call it Relevance(), that returns a relevance score from 0 — not relevant, to some positive number.
For example, imagine that we want to recommend a movie according to its genre. The Relevance() function orders movie genres according to a defined rule. For visualization purposes, let’s say that we have a list of genres with relevance scores: [A₃, T₁, D₀] where A - action, T - thriller, D - drama. The subscript number defines the relevance scores for each element.
Traditional DCG and Its Limitations
Among the variety of measures, discounted cumulative gain (DCG) is the most notable. It is used during information retrieval (IR) competitions, including annual TREC competitions. DCG is defined by the following formula:
DCG = Σ(i=1 to n) Relevance(xᵢ) / log₂(i+1)
While normalized DCG (nDCG) improves interpretability by normalizing scores, it has several drawbacks:
- Non-zero minimum scores: The measure never produces “0” for completely wrong orderings
- Subgroup transitivity issues: Doesn’t handle permutations within equal-relevance groups properly
- Score inflation: Can produce scores above 1.0 when using estimated relevance values
Introducing RankDCG
RankDCG was designed to address these problems. The main idea of this measure is to:
- Normalize scores to be in the range from 0 to 1
- Add transitive property to subgroups (permutations within same-relevance groups are equal)
- Abstract from relevance scores (relative ordering matters, not absolute values)
Formally stated:
RankDCG = Σ(i=1 to n) relevance'(xᵢ) / reversed_relevance(i)
Where relevance'() is derived by counting unique relevance scores and reversed_relevance() provides appropriate discounting factors with subgroup position correction.
Key Advantages
By adding these two functions to the definition, the measure addresses all the limitations mentioned above in a consistent manner. By using RankDCG, researchers will be able to:
- Better understand their results with consistent 0-1 scoring
- Design algorithms with much higher precision
- Handle complex ranking scenarios that traditional measures struggle with
Implementation and Resources
RankDCG delivers better results on wider types of problems compared to conventional measures. Evaluating the results of ordering is a hard task where conventional measures fail to deliver consistent results on a wide range of problems.
Research Paper: RankDCG: An Evaluation Measure for Ranking Algorithms
Python Library: RankDCG GitHub Repository
Poster: RankDCG Poster PDF
This work provides researchers and practitioners with a more robust tool for evaluating ranking algorithms across diverse applications, from search engines to recommendation systems.